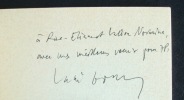129 books for « r godel »Edit

‎Le Maître de Nô‎

‎Albin Michel/ question de n° 78 1989 15x23x1cm. 1989. Broché. 157 pages. Bon Etat intérieur propre‎

‎Godel's Theorem in Focus , (Kurt Gödel in sharper focus - On formally undecidable propositions of Principia Mathematica and related systems I (1931) - The work of Kurt Godel - The reception of Godel's incompleteness theorems - Kurt Godel : Conviction and caution - On the significance of consistency proofs - On interpreting Godel's second theorem -Wittgenstein's remarks on the significance of Godel's theorem)‎

‎Routledge, London and New York , Philosophers in Focus Series Malicorne sur Sarthe, 72, Pays de la Loire, France 1989 Book condition, Etat : Très Bon paperback, editor's full yellow and grey printed wrappers In-8 1 vol. - 270 pages‎

‎ reprinted edition, 1989 Contents, Chapitres : Contents, Preface, Acknowledgments, ix, Text, 261 pages - John W. Dawson : Kurt Gödel in sharper focus - Kurt Godel : On formally undecidable propositions of Principia Mathematica and related systems I (1931) - Stephen C. Kleene : The work of Kurt Godel - John J. Dawson : The reception of Godel's incompleteness theorems - Solomon Feferman : Kurt Godel : Conviction and caution - Michael D. Resnik : On the significance of consistency proofs - Michael Detlefsen : On interpreting Godel's second theorem - S.G. Shanker : Wittgenstein's remarks on the significance of Godel's theorem - Index near fine copy, no markings‎

‎Le théorème de Gödel , Traduction de l'anglais et de l'allemand par Jean-Baptiste Scherrer (Gödel's Proof)‎

‎Seuil , Sources du Savoir Malicorne sur Sarthe, 72, Pays de la Loire, France 1989 Book condition, Etat : Bon broché, sous couverture imprimée éditeur blanche et rouge In-8 1 vol. - 184 pages‎

‎Quelques figures dans le texte en noir et blanc 1ere traduction en français, 1989 Contents, Chapitres : Préface- 1. Ernest Nagel et James R. Newman : La démonstration de Godel : Introduction - Le problème de la consistance - Les démonstrations de la consistance absolue - La systématisation de la logique formelle - Exemple de démonstration de consistance absolue - Le concept de projection et son application en mathématiques - La démonstration de Gödel (La numération de Gödel - L'arithmétisation des métamathématiques - Le coeur du raisonnement de Gödel) - Conclusions et appendices - 2. Kurt Gödel : Sur les propositions formellement indécidables des Principia Mathematica et des systèmes apparentés - 3. Jean-Yves Girard : Le champ du signe ou la faillite du réductionnisme : La tentation mécaniste : Hilbert - La chute de la maison Hilbert - Quand même ! - Postérité de Gödel - La gödélite - Bibliographie - Index de la démonstration de Gödel - Kurt Gödel, né le 28 avril 1906 à Brünn et mort le 14 janvier 1978 à Princeton (New Jersey), est un logicien et mathématicien autrichien naturalisé américain. Son résultat le plus connu, le théorème d'incomplétude de Gödel, affirme que n'importe quel système logique suffisamment puissant pour décrire l'arithmétique des entiers admet des propositions sur les nombres entiers ne pouvant être ni infirmées ni confirmées à partir des axiomes de la théorie. Ces propositions sont qualifiées d'indécidables. Gödel a également démontré la complétude du calcul des prédicats du premier ordre. Il a aussi démontré la cohérence relative de l'hypothèse du continu, montrant qu'elle ne peut pas être réfutée à partir des axiomes admis de la théorie des ensembles, en admettant que ces axiomes soient cohérents. Il est aussi à l'origine de la théorie des fonctions récursives. Il publie ses résultats les plus importants en 1931 à l'âge de 25 ans, alors qu'il travaille encore pour l'université de Vienne (Autriche). (source : Wikipedia) couverture à peine jaunie avec d'infimes traces de pliures aux coins des plats, sans aucune gravité, intérieur frais et propre, cela reste un bon exemplaire de cet ouvrage de référence sur le théorème de Gödel qui est un des fondements de la logique mathématique moderne - nb : grand format de la 1ere édition française avec l'article de Jean-Yves Girard, il ne s'agit pas de la réédition en poche‎

‎Über eine bisher noch nicht benützte Erweiterung des finiten Standpunktes. (In: Dialectica, volume 12, pp.280-87). - [GÖDEL'S FINAL PAPER]‎

‎Neuchâtel, Dialectica, 1958. 8vo. Original printed wrappers. The entire issue 47/48 offered here. Uncut and unopened.‎

‎First edition of Gödel's 'Dialectica-paper' in which he presented his consistency proof for arithmetic. In 1931 Gödel formulated and proved his second incompleetness theorem" that the consistency of Peano arithmetic cannot be proved using Peano arithmetic itself or any of its direct extensions. The title of Gödel's famous 1931 paper (Über formal unentscheidbare Sätze der Principia Mathematica und verwandter Systeme I) states that it is the first part of several papers. Gödel mentions, in a footnote, that the second part of his paper will deal with the source of the incompleteness of formal systems using the theory of types. But no actual continuation of Gödel's 1931 paper ever appeared. However, in his 1958 ""Dialectica-paper"" (the offered item) Gödel showed how type theory can be used to give a consistency proof for arithmetic. In this paper Gödel furthermore discussed some of the philosophical implications of his results. Paul Bernays thought highly of this paper, and planned to publish an English translation, but during the revision of the paper Gödel became dissatisfied with the philosophical introduction and rewrote it completely. When the proof sheets of the revised paper arrived from the printer, Gödel once again became unpleased with the sections concerning his philosophical views. He never returned the proof sheets. The issue offered, which is a festschrift on the occasion of Paul Bernay's 70th birthday, furthermore contains original contributions by Ackermann, Carnap, Curry, Fraenkel, Robinson, Skolem.‎

‎Über Vollständigkeit und Widerspruchsfreiheit (+) Eine Eigenschaft der Realisierungen des Aussagenkalküls.‎

‎Leipzig & Berlin, B.G. Teubner, 1932. 8vo. In the original wrappers. In ""Ergebnisse eines mathematischen Kolloquiums, unter Mitwirkung von Kurt Gödel und Georg Nöbeling, herausgegeben von Karl Menger, Heft 3"". A near mint copy, Pp. 12-13"" Pp. 20-21. [Entire volume: 26 pp].‎

‎First printing of these two important papers both closely related to Gödel landmark paper Über formal unentscheidbare Sätze"". Here Gödel applies the extensions of the incompleteness theorems to a wider class of formal systems : ""is already the more modern first-order Peano arithmetic, the system in which Godel in his abstract described his incompleteness results. The passage [in the present paper] envisages the introduction of higher-type variables, which would have the effect of re-establishing the system P, but as one proceeds to higher and higher types, that ""all the [unprovable] propositions constructed are expressible in Z (hence are number-theoretic propositions)"" is an important point about incompleteness. The last sentence of the [1932] passage is Godel's first remark on set theory of substance, and significantly, his example of an ""axiom of cardinality"" to take the place of type extensions is essentially the one that both Abraham Fraenkel [1922] and Thoralf Skolem [1923] had pointed out as unprovable in Ernst Zermelo's [1908] axiomatization of set theory and used by them to motivate the axiom of Replacement. "" (Kanamori, Gödel and Set Theory). ""By invitation, in October 1929 Gödel began at tending Menger's mathematics colloquium, which was modeled on the Vienna Circle. There in May 1930 he presented his dissertation results, which he had discussed with Alfred Tarski three months ear lier, during the latter's visit to Vienna. From 1932 to 1936 he published numerous short articles in the proceedings of that colloquium (including his only collaborative work) and was coeditor of seven of its volumes. Gödel attended the colloquium quite regularly and participated actively in many discus sions, confining his comments to brief remarks that were always stated with the greatest precision."" (DSB)‎

‎[Bericht uber die 2. Tagung für Erkenntnislehre der exakten Wissenschaften Königsberg 1930]. Die Logizistische Grundlegung der Mathematik + Die intuitionistische Grundlegung der Mathematik + Die formalistische Grundlegung der Mathematik. [In: Erkenntn... - [ENDING THE FOUNDATIONAL CRISIS OF MATHEMATICS]‎

‎Leipzig, Felix Meiner, 1931. The entire volume present. 8vo. Orig. printed green wrappers. Sunning to spine, and a bit of soiling and minor wear to front wrapper w. minor loss of upper layer of paper at two pages, not gone through paper. A few leaves w. marginal markings, quite discreet. Library marking to inside of front wrapper, library stamp to title-page (Mathematical Institute of the University of Amsterdam). Overall a fine and nice copy. Pp. (91) - 105 + (106) - 115 + (116) - 121. The entire volume: (2) pp., Pp. (91) - 190.‎

‎First edition of the Erkenntnis-volume from the Königsberg congress of 1930, where Gödel introduced his incompleteness results and Carnap, Heyting and von Neumann held the seminal papers (here printed for the first time) that ended the ""Grundlagenkrise der Mathematik"" (foundational crisis of mathematics). It is also in this volume that the seminal discussions following Gödel's announcements of his results are printed for the first time (""Discussion on the Foundation of Mathematics"", between Gödel, von Neumann, Carnap, Hahn, Reidemeister, Heyting, and Scholz) (Gödel, Collected Works, 1931a) as well as the article which inaugurated the logicist foundation of mathematics, in which the modern sense of ""logicism"" is introduced (Carnap's contribution).In Königsberg in September 1930, Gödel presented his incompleteness results, a landmark in mathematical logic, at the second congress of scientific epistemology, -a congress which proved to be a turning point in the history of philosophical and mathematical logic. It is the papers presented at this congress which are printed in the present volume, apart from the contributions by Gödel and Scholtz (which were printed elsewhere) together with the seminal discussions that followed the presentation of the papers. The groundbreaking papers that are printed here include Carnap's ""Die Logizistische Grundlegung der Mathematik"", which furthermore introduced the modern sense of the term ""logicism"", Arend Heyting's ""Die intuitionistische Grundlegung der Mathematik"" and Johann von Neumann's ""Die formalistische Grundlegung der Mathematik"" as well as papers by Neugebauer, Reichenbach and Heisenberg. The present papers, as well as the following discussion, mark a turning point in the history of logic and a cornerstone in the future development of the field. The so-called ""Foundational Crisis of Mathematics"" was a phase within mathematics begun in the early 20th century due to the search for proper foundations of mathematics and the uncertainty of this quest, which was supported by the many difficulties that philosophy of mathematics faced at the end of the 19th and beginning of the 20th century . The crisis took its actual beginning with the publication of Russell's ""principles of Mathematics"" of 1903, culminated in the 1920'ies with the main advocates of Formalism and Intuitionism respectively, Hilbert and Brouwer, in what is called the ""foundational struggle of mathematics"", and ended with the present volume in 1931, following the congress of 1930.With the discovery of non-Euclidean geometry in the 18th century, it became evident that not only one sort of mathematics was possible, and even that some propositions could be true in one mathematical system, but false in another. This was the actual basis for the awareness of a mathematical foundation in the mathematical public, which again was the basis for the fact that the question of the foundation of mathematics could develop -and could develop into an actual crisis. During the first 30 years of the 20th century, almost all great mathematicians worked on their answer to the question of the correct foundation of mathematics, and thus it came to a crisis that developed into a struggle. It is this struggle and crisis that Carnap, Heyting and von Neumann break in 1930, where they present the three great positions of the struggling years: logicism (Carnap), intuitionism (Heyting) and formalism (von Neumann), and it is these three papars that pave the way for the discussion that follows, ""Diskussion zur Grundlegung der Mathematik"", between Gödel, Hahn, Carnap, Heyting, von Neumann, Reidemeister, and Scholz. They all presented their positions in the most conciliatory manner, out of the comprehension that all parties who had contributed to the crisis had also contributed because they wanted to solve it, and because they were also searching for the best possible foundation. It is also this comprehension that Hilbert takes over, when he, in his program, sets out to prove the contradiction-freedom of infinite mathematics on the basis of finite arithmetic.Thus, the seminal papers in the present volume once and for all ended the foundational crisis of mathematics and any fear of new antinomies.‎

‎Die Vollständigkeit der Axiome des logischen Funktionskalküls. [In: Monatshefte für Mathematik und Physik, XXXVII. Band]. - [THE COMPACTNESS THEOREM]‎

‎[Leipzig, 1930). 8vo. Stapled extract. Some flossing to inner margin, probably from when extracted, far from affecting text. Handwritten indication of the journal, from which it is extracted, in pencil, on top of first page. Pp. (349) - 360.‎

‎The scarce first printing of this seminal paper, in which Gödel, the greatest logician since Aristotle, proves for the first time the compactness theorem, which is of the greatest importance to the development of model theory, as it provides a useful method for constructing models of any set of sentences that is finitely consistent. The compactness theorem is used by Gödel to derive a generalization of the completeness theorem. The present highly important and influential paper constitutes a revised and shortened version of Gödel's doctorial dissertation, published the same year, in which he showed that every valid formula of first-order logic is provable and, moreover that each axiom of first-order logic is independent (the first of which is referred to as Gödel's completeness theorem). In this journal version he, in addition to that proved in the dissertation, also proved his highly influential compactness theorem (which states that a set of first-order sentences has a model if and only if every finite subset of it has a model). ""G settled the [problem] of completeness (positively) in the summer and wrote up the result as his dissertation, which was finished by July. A revised version was received by the editor of ""Monatshefte"" on 22 October and published 1930"" a main addition was what is now known as ""Compactness theorem"". G received his doctoral degree on 6 February 1930. He presented his result in Menger's colloquium on 14 May and in Königsberg on 6 September 1930."" (Wang, Reflections on Kurt Gödel). ""The Compactness Theorem was extended to the case of uncountable vocabularies by Maltsev in 1936, from which the Upward Löwenheim-Skolem theorem immediately follows. The Compactness Theorem would become one of the main tools in the then fledgling subject of model theory."" (SEP).From the library of the highly important Danish logician and philosopher Jørgen Jørgensen (1894-1969), who was an active collaborator with the logical positivists from the Vienna Circle. After Hans Hahn's death he became editor of the series of the Vienna Circle, the ""Einheitswissenchaft"" (""Unified Science""), and later he collaborated on the International Encyclopedia, to which he contributed with the essay ""The Development of Logical Empiricism"", 1951. Jørgensen is also widely recognized for his three volume work ""Treatise of Formal Logic"" Its Evolution and Main Branches, with its Relations to Mathematics and Philosophy"", 1931.Apart from the paramount importance of the paper, it is also of the utmost rarity, as evidenced by the fact that it is neither present in the collection of Honeyman, Barchas, Haskell Norman, nor Hook & Norman: Origins of Cyberspace, and furthermore, the paper has not been up for sale on any of the major auction houses for at least the last 50 years.‎

‎Ein Spezialfall des Entscheidungsproblems der theoretischen Logik. - [INCOMPLETENESS FROM THE STANDPOINT OF FIRST-ORDER LOGIC]‎

‎Leipzig & Berlin, B.G. Teubner, 1932. 8vo. A mint copy, in the original wrappers, still contained in the original plastic protection. In ""Ergebnisse eines mathematischen Kolloquiums, unter Mitwirkung von Kurt Gödel und Georg Nöbeling, herausgegeben von Karl Manger, Heft 2"". Pp. 27-28. [Entire volume: 38 pp].‎

‎First edition of Gödel's important paper, which constitutes a supplement to his ""Die Vollständigkeit der Axiome des logischen Funktionskalküls"" (1930). In the present paper, Gödel seminally formulates his earlier incompleteness results from the standpoint of first-order logic, thereby contributing substantially to modern mathematical logic.""In 1932 Godel published his formulation of the incompleteness results from the standpoint of first order logic. If number theory is regarded as a formal system in first-order logic, then the above results about incompleteness and unprovability of consistency apply to S. If, however, S is extended by variables for sets of numbers, for sets of sets of numbers, and so on (together with the corresponding comprehension axioms), then we obtain a sequence of systems S"" the consistency of each system is provable in all subsequent systems. But in each subsequent system there are undecidable propositions. Going up in type in this way, he noted, corresponds in a type-free system of set theory to adding axioms that postulate the existence of larger and larger infinite cardinalities. This was the beginning of Gödel's interest in large cardinal axioms, an interest that he elaborated in 1947 in regard to the continuum problem."" (DSB).The issue contains several papers by Karl Menger.‎

‎An Introduction to Gödel's Theorems , Cambridge Introductions to Philosophy‎

‎Cambridge University Press , Cambridge Introductions to Philosophy Malicorne sur Sarthe, 72, Pays de la Loire, France 2008 Book condition, Etat : Très bon paperback, editor's red and yellow wrappers, illustrated by a multicolor illustration grand In-8 1 vol. - 375 pages‎

‎many black and white text-figures 2nd reprinted edition, 2008 Contents, Chapitres : Contents, Preface, xiv, Text, Further reading, Bibliography, Index, 361 pages - What Gödel's theorems say Decidability and enumerability Axiomatized formal theories Capturing numerical properties - The truths of arithmetic - Sufficiently strong arithmetics Interlude : Taking stock - Two formalized arithmetics What Q can prove - First-order Peano arithmetic - Primitive recursive functions Capturing p.r. functions - Q is p.r. adequate Interlude : A very little about principia - The arithmetization of syntax PA is incomplete - Gödel's first theorem Interlude : about the first theorem Strengthening the first theorem The diagonalization Lemma Using the diagonalization lemma Second-order arithmetics - Interlude : Incompleteness and Isaacsons conjecture - Gödel's second theorem for PA The derivability conditions Deriving the derivability conditions Reflections - Interlude : About the second theorem µ-recursive functions Undecidability and incompleteness Turing machines Turing machines and recursiveness Halting problem The church-turing thesis Proving the thesis ? - Looking back near fine copy, no markings‎

‎The Consistency of the Axiom of Choice and of the Generalized Continuum-Hypothesis (+) Consistency-proof for the Generalized Continuum-Hypothesis. - [THE CONSISTENCY OF SET THEORY]‎

‎Washington, 1938 & 1939. Royal8vo. 2 volumes, uniformly bound in contemporary full cloth with gilt lettering to spine. Exlibris to front paste down. In ""Proceedings of the National Academy of Science"", vol. 24 and 25. Fine and clean. Pp.556-57" Pp. 220-24). [Entire volumes: VII, 572 pp. VII, 661 pp].‎

‎First edition of arguable Gödel's most important publications only second to his incompleteness theorem. The first problem of Hilbert's famous 1900 address asks for a proof of Cantor's continuum hypothesis. Hilbert considered this problem one of the most important problems confronting the mathematical world. As a first step towards such a proof Ernst Zermelo proved in 1904 another hypothesis by Cantor, namely that every set can be well ordered. In his proof Zermelo introduced a necessary tool which later became known as the axiom of choice. Because of its non-constructive nature this axiom, and the continuum hypothesis, became the object of much controversy in the mathematical community. Gödel's results on this topic are, besides his completeness and incompleteness theorems, his most celebrated. During the autumn terms of 1938 and 1939 Gödel delivered a series of lectures at the Institute for Advanced Study, in which he proved that the axiom of choice and the generalized continuum hypothesis are consistent with the other axioms of set theory if these axioms are consistent. ‎

‎Vahé Godel. ‎

‎Fribourg, éditions universitaires, collection Cristal, 1981. In-8 broché, couverture illustrée. Second plat un peu taché, pour le reste en belle condition. ‎

‎Entretien et choix de textes. Exemplaire agrémenté d'un envoi autographe signé de Vahé Godel. * La librairie la Bergerie est sur le point de déménager - c'est la raison pour laquelle nous vous proposons jusqu'à la fin de l'année une remise de 10% sur tout le stock (pour les ouvrages encore en rayons) et de 20% sur ceux qui, déjà mis dans les cartons de déménagement, ne pourront être livrés qu'en début d'année prochaine. La remise sera déduite des prix affichés *‎

‎Roger Godel. Recherche d'une foi. Cités et univers de Platon‎

‎Générique Broché D'occasion bon état 01/01/1942 100 pages ‎

‎Roger Godel. Platon à Héliopolis d'Égypte : . Post-face de François Daumas‎

‎Générique Broché D'occasion bon état 01/01/1956 100 pages ‎

‎Ergebnisse eines mathematischen Kolloquiums, unter Mitwirkung von Kurt Gödel und Georg Nöbeling, herausgegeben von Karl Menger, Heft 1.‎

‎Leipzig & Berlin, Teubner, 1931. 8vo. In the original printed wrappers still contained in the original plastic protection. A little rust coming of the staples as usual. A near mint copy. 31 pp.‎

‎The rare first appearance of the first publication (Heft 1) of the proceedings of the famous mathematics colloquium founded by Karl Menger, which came to include some of the 20th century most influential and important mathematicians.‎

‎Amenophis 5 « Revue sous bandelette » ‎

‎Bruxelles, Amenophis, n°5 janvier 1970. Broché, 20 cm x 21 cm, 42 pages, illustrations noir & blanc in et hors-texte. Texte et illustrations de Pierre Chabert, Vahe Godel, Jose Goemaere, Marie-Claire Gouat, Robert Kayser, Jacques Lepage, Jean-Marie Le Sidaner, Lucifer, André Miguel, Cécile Miguel, Jean-Claude Moineau, André Morlain, Michèle Perfetti, Christian Prigent, Gaston Puel, Pierre Puttemans, Vincent Rougier, jean-Luc Steinmetz, Christian Tobas, Albin Tzaut, Michel Vachey, Jean-Pierre Verheggen. Très bon état ‎

‎Vahé Godel: Exhumer le dédale, par Jean-Marie Le Sidaner. Le Courrier du centre international d’études poétiques, n°107, 1975.‎

‎ Bruxelles: Maison internationale de la poésie, président: Etienne Souriau, direction Fernand Verhesen, 1975. Un volume 16x23cm agrafé de 20 pages. Bon état. ‎

‎Créée à l’occasion des Biennales internationales de poésie à Bruxelles en 1954, cette importante revue d’analyse critique et poétique présente des essais, des poèmes inédits, des traductions et des hommages. Plus de 200 numéros seront édités jusqu’au début des années 2000. ‎

‎Essais sur l'experience liberatrice‎

‎Gallimard Broché D'occasion bon état 01/01/1952 150 pages ‎

‎L'AUBE ne ressemble pas à l'aube‎

‎Abraxas Broché D'occasion bon état 01/01/1981 150 pages ‎

‎Terre Ciel Visages. Sculptures et Photographies à la pointe d’argent de Boris Lejeune.‎

‎Éditions de la Différence - Coll. Le Miroir Oblique 1995 In-4 broché 27,5 cm. Bon état d’occasion.‎

‎Sculptures et Photographies à la pointe d’argent de Boris Lejeune. Textes Gloaguen, Alexis ; Godel, Vahé ; Guillevic Bon état d’occasion ‎

‎Zones frontières. ‎

‎Essertines-sur- Rolle, éditions Demoures, 1998. In-8, cartonnage illustré. Compositions en noir et en couleurs de Jean Zuber. ‎

4 Images

‎"Autour de douze beaux poèmes de Vahé Godel qui explorent les Zones frontières – celles de la mémoire qui s'effiloche, du délire du moribond, des cités anéanties, du rêve «aquarium de la nuit» selon Hugo, du lierre qui enlace un tronc comme les bandelettes la momie – autour, donc, du vide et de la perte, Jean Zuber (Biennois devenu Parisien, admirateur des cultures amérindiennes, aborigènes, africaines) propose des échos silhouettés, minimalistes et tragiques, deux chaises vides, une tache noire trouée de blanc, un avion fantôme entre une lune jaune et une lune bleue." in Le Temps, 12 décembre 1998. * La librairie la Bergerie est sur le point de déménager - c'est la raison pour laquelle nous vous proposons jusqu'à la fin de l'année une remise de 10% sur tout le stock (pour les ouvrages encore en rayons) et de 20% sur ceux qui, déjà mis dans les cartons de déménagement, ne pourront être livrés qu'en début d'année prochaine. La remise sera déduite des prix affichés *‎

‎LE THEOREME DE GODEL‎

‎SEUIL. 1989. In-8. Broché. Bon état, Couv. convenable, Dos satisfaisant, Intérieur frais. 178 pages.. . . . Classification Dewey : 800-LITTERATURE (BELLES-LETTRES)‎

‎ Classification Dewey : 800-LITTERATURE (BELLES-LETTRES)‎

‎Homme parmi les Hommes.‎

‎Paris Seghers, Poésie 58, coll. "PS 522" 1958 1 vol. broché plaquette in-12, brochée, couverture à rabats, 35 pp. Bon état.‎

‎PORTES D'ISHTAR. Dialogues et images cinématographiques.‎

‎ Le Caire, Imprimerie de l'Institut français d'Archéologie orientale, 1945. In-4, reliure d'édition pleine toile écrue gris pâle, 143pp, texte imprimé en rouge et noir, édition originale, un des 100 ex. du tirage numéroté (N° 80), seul grand papier. Très bel et important envoi autographe de l'auteur à Mr. de Fooz. ‎

‎Médecin cardiologue en Égypte dans les années 1950 et au Liban, son intérêt pour les philosophies orientales et grecque l'a incité à tenter une réconciliation originale entre la pensée indienne et celles de Socrate et Platon. Il était l'époux d'Alice Godel, mère d'Andrée Chedid. cf. wikipédia. Reliure défraîchie, avec de minuscules salissures, l'intérieur est très frais. - Frais de port : -France 6,9 € -U.E. 9 € -Monde (z B : 15 €) (z C : 25 €) ‎

‎Vahé Godel. Collection Cristal. Volume 2. ‎

‎Fribourg, Ed. Univers. Fribourg, 1981, gr. in-8°, 136 p., brochure originale illustrée (par Mme Koop).‎

‎Roger Godel aux colloques Orient-Occident- à Beyrouth, avril-mai 1959‎

‎Beyrouth , Centre de diffusion libanais / ministère de l'orientation et de l'information , 1963, Grand in huit , 206 pp, très bon état, complet de l'errata, photo en frontispice,‎

‎. ‎